Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element a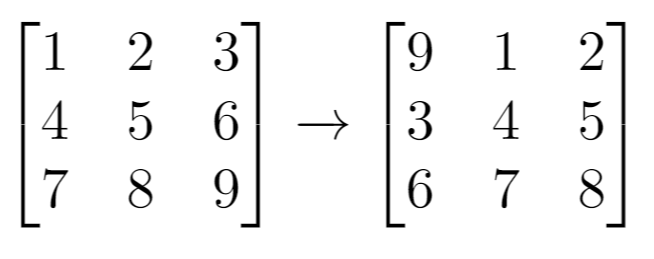t grid[i][j] becomes at grid[i][j + 1].
• Element at grid[i][n - 1] becomes at grid[i + 1][0].
• Element at grid[n - 1][n - 1] becomes at grid[0][0].
  Return the 2D grid after applying shift operation k times.

Example 1:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2: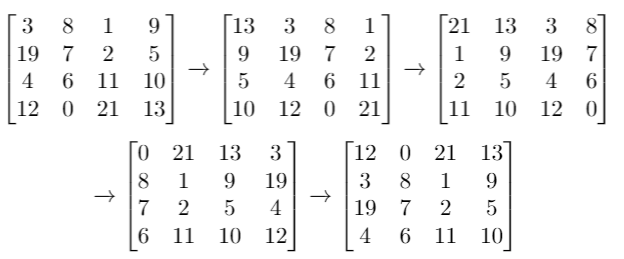

Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

* m == grid.length
* n == grid[i].length
* 1 <= m <= 50
* 1 <= n <= 50
* -1000 <= grid[i][j] <= 1000
* 0 <= k <= 100

解析

此題給予一個m * n的矩陣及一正整數k，要求陣列元素在移動k步之後形成的陣列。

解法一：可以先使用雙向佇列存進陣列的所有元素，在使用Python的rotate函式移動陣列元素，最後將原陣列的元素更新成佇列裡的元素即可達成題目所求，不過此方法需額外建立雙向陣列提高了空間複雜度。

解法二：可以把元素移動k步這個步驟視為將後面k個元素挪到陣列前面，進而重組陣列，此方法的空間複雜度為O(1)。

解法一

from collections import deque
class Solution:
    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        # Minimum movement needed
        move = k % (len(grid) * len(grid[0]))
        if move == 0:
            return grid
        res = deque()
        for i in grid:
            for j in i:
                res.append(j)
        res.rotate(move)
        col = len(grid[0])
        for i in range(len(res)):
            grid[i//col][i % col] = res[i]
        return grid 

解法二

class Solution:
    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        col, nums = len(grid[0]), sum(grid, [])
        k = k % len(nums)
        nums = nums[-k:] + nums[:-k]
        return [nums[i:i+col] for i in range(0, len(nums), col)]

備註

希望透過記錄解題的過程，可以對於資料結構及演算法等有更深一層的想法。
如有需訂正的地方歡迎告知，若有更好的解法也歡迎留言，謝謝。